Les enquêtes nationales et internationales mettent régulièrement en lumière les difficultés des élèves français en résolution de problèmes en comparaison des élèves des pays économiquement comparables. Les problèmes pour lesquels ces difficultés apparaissent sont généralement des problèmes en deux ou trois étapes, comme l'exercice suivant qui a été proposé en 2015, dans le cadre de l'évaluation Timss (1), aux élèves de fin de CM1.

Une bouteille de jus de pomme coûte 1,87 zeds.

Une bouteille de jus d'orange coûte 3,29 zeds.

Julien a 4 zeds.

Combien de zeds Julien doit-il avoir en plus pour acheter les deux bouteilles ?

A. 1,06 zeds                     B. 1,16 zeds          C. 5,06 zeds          D. 5,16 zeds

Pour ce problème, les élèves français ont obtenu le plus faible taux de réussite des pays de l'Union européenne participants, avec un score de 42 %, alors que le tiers des autres pays de l'Union européenne ont obtenu des scores de réussite moyens entre 62 % et 70 % et qu'un pays comme Singapour a même atteint 79 % (2).

Cet exemple met en lumière les difficultés qu'il convient de résorber. La résolution de problèmes doit être au cœur de l'activité mathématique des élèves tout au long de la scolarité obligatoire. Elle participe du questionnement sur le monde et de l'acquisition d'une culture scientifique, et par là contribue à la formation des citoyens. Elle est une finalité de l'enseignement des mathématiques à l'école élémentaire, mais aussi le vecteur principal d'acquisition des connaissances et des compétences visées.

L'objet de la présente note de service est de contribuer à la mise en place d'un enseignement construit pour développer l'aptitude des élèves à résoudre des problèmes. Cela nécessite de conduire, année après année, et dès le plus jeune âge, un travail structuré et régulier pour faire acquérir aux élèves les connaissances et compétences leur permettant :

- de comprendre le problème posé ;

- d'établir une stratégie pour le résoudre, en s'appuyant sur un schéma ou un tableau, en décomposant le problème en sous-problèmes, en faisant des essais, en partant de ce que l'on veut trouver, en faisant des analogies avec un modèle connu ;

- de mettre en œuvre la stratégie établie ;

- de prendre du recul sur leur travail, tant pour s'assurer de la pertinence de ce qui a été effectué et du résultat trouvé, que pour repérer ce qui a été efficace et ce qui ne l'a pas été afin de pouvoir en tirer profit pour faire des choix de stratégies lors de futures résolutions de problèmes.

1 - Un enseignement structuré et explicite de la résolution de problèmes

Enseigner la résolution de problèmes nécessite de concevoir une progressivité pour les problèmes proposés, en commençant par des problèmes additifs élémentaires en une étape, avant de proposer des problèmes plus complexes (multiplicatifs élémentaires) et d'augmenter progressivement le nombre d'étapes des problèmes proposés.

Au sein d'une même catégorie de problèmes, une progressivité doit être établie : par exemple, au sein des problèmes additifs élémentaires en une étape, les nombres en jeu ou l'aspect dynamique ou non de la situation peuvent ajouter de la complexité pour les élèves. Les quatre problèmes suivants, bien que faisant tous appel à une soustraction et à des nombres inférieurs à 50, sont d'une difficulté inégale pour les élèves.

- Léo et Lucie ont 43 billes à eux deux. Léo a 6 billes. Combien Lucie a-t-elle de billes ?

- Lucie avait 43 billes ce matin. Elle a perdu 6 billes pendant la récréation. Combien a-t-elle de billes maintenant ?

- Lucie avait 43 billes ce matin. Elle a perdu 37 billes pendant la récréation. Combien a-t-elle de billes maintenant ?

- Lucie a gagné 6 billes à la récréation. Maintenant elle a 43 billes. Combien de billes avait-elle avant la récréation ?

Les différents types de problèmes se résolvant par une même opération doivent être rencontrés et explicités aux élèves, selon une programmation réfléchie tenant compte des différents niveaux de difficulté et de l'impératif de ne pas laisser s'installer une vision réductrice du sens des opérations. La soustraction, par exemple, ne doit pas être assimilée à la seule situation de retrait.

Un enseignement explicite de la résolution de problèmes doit s'appuyer sur des temps spécifiques qui structurent les savoirs et compétences travaillés : des références construites avec les élèves et notées dans les cahiers prévus à cet effet (cahiers de référence en mathématiques) permettent de garder traces de l'aboutissement du travail effectué. Ces références peuvent être des résolutions de problèmes types sur lesquelles les élèves pourront s'appuyer lors de séances ultérieures pour résoudre correctement d'autres problèmes proposés. Références « construites avec les élèves » ne signifie en rien qu'il s'agit de productions imparfaites ; bien au contraire, il s'agit de modèles dont les élèves pourront s'inspirer pour leurs propres travaux. Ces exemples-types doivent servir de références systématiques lors des résolutions de problèmes ultérieures (« c'est comme... »). Idéalement, ces références seront communes à l'école, voire au réseau d'écoles, pour permettre de les utiliser pendant plusieurs années.

La formalisation de ces exemples-types doit être l'occasion d'introduire des représentations, sous forme de schémas bien adaptés, permettant la modélisation des problèmes proposés. Ces représentations sont systématiquement utilisées lors des résolutions de problèmes menées face à la classe, afin de servir de référence aux élèves. Elles ne sont bien sûr jamais rendues obligatoires (en particulier pour les élèves en réussite qui n'en ont pas besoin), mais doivent servir de point d'appui, lors des séances d'enseignement, avec les élèves rencontrant des difficultés lors de la résolution d'un problème.

L'objectif n'est pas d'établir un catalogue détaillé de typologies de problèmes pouvant exister, dont l'usage serait inopérant pour les élèves, mais au contraire de réunir les problèmes dans des catégories aussi larges que possible en faisant des analogies, par exemple, entre les problèmes pouvant s'appuyer sur les mêmes représentations. Ainsi, les quatre exemples de problèmes proposés ci-dessus peuvent correspondre à un même « modèle » : indépendamment de l'aspect dynamique ou non de la situation, il s'agit en effet, à chaque fois, d'un ensemble partagé en deux parties. Le cardinal de l'ensemble et celui d'une partie sont connus et le problème a pour objet de déterminer le cardinal de la seconde partie.

Les représentations schématiques associées à ces quatre problèmes peuvent ainsi prendre la même forme et correspondre au même « modèle » :

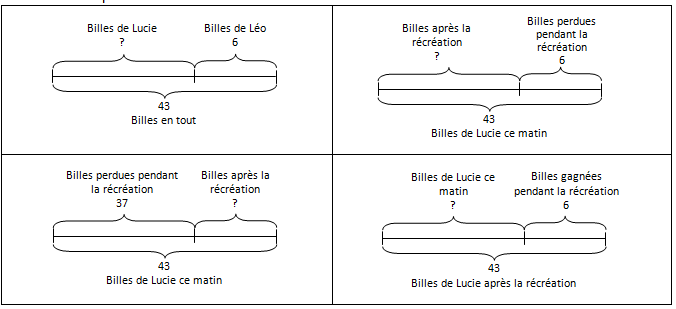
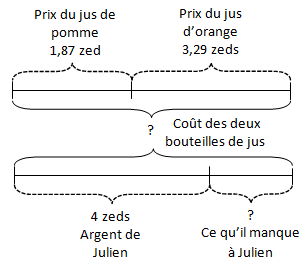
Comme on peut le voir ci-dessus, la résolution du problème issu de l'évaluation Timss peut s'appuyer sur une représentation schématique similaire à celle utilisée dans les quatre problèmes donnés en exemples au point 1. La compréhension peut ainsi en être facilitée.

D'autres types de représentations pouvant aider les élèves à la modélisation des problèmes à résoudre peuvent être proposés : dessins, diagrammes, graphiques, etc.

2 - Les problèmes à soumettre aux élèves 

L'exemple du problème issu de l'évaluation Timss donné en introduction met en lumière les difficultés des élèves français à résoudre des problèmes numériques en plusieurs étapes. L'objectif prioritaire doit donc être de former les élèves, très tôt, à la résolution de problèmes élémentaires de cette nature.

Tout en ne négligeant pas le travail préalable sur les problèmes en une étape, briques élémentaires sur lesquelles pourront s'appuyer les élèves pour résoudre les problèmes en plusieurs étapes, il est important de proposer des problèmes en deux étapes dès le début du cycle 2 (3) : l'objectif visé est de ne pas laisser les élèves penser que résoudre des problèmes se limite à « trouver la bonne opération » ou « avoir de la chance » en prenant les deux nombres de l'énoncé et en choisissant une opération au hasard.

Des problèmes qui ne sont ni additifs ni multiplicatifs peuvent également être proposés aux élèves, en particulier au cycle 3, comme, par exemple, des problèmes qu'il faut résoudre par la méthode essai-erreur (4)

Ces problèmes ne doivent pas apparaître de façon isolée, mais être inscrits dans des séquences d'apprentissage au sein desquelles plusieurs problèmes pouvant être résolus par la méthode visée sont proposés. Il convient d'assigner à chaque séquence un objectif d'apprentissage précis ; dans l'exemple de la méthode essai-erreur, il s'agit d'apprendre à chercher, en tâtonnant, en faisant des essais successifs. L'acquisition de la méthode enseignée ou de la démarche visée, dont les cahiers de référence gardent la mémoire, devra ensuite être renforcée par une rencontre régulière de problèmes permettant de la mettre en œuvre au cours des périodes et des années suivantes.

3 - La mise en œuvre dans la classe 

L'enseignement de la résolution de problèmes peut s'appuyer sur des temps d'échanges collectifs, permettant d'émettre des hypothèses, d'élaborer collectivement des stratégies, de confronter des idées et d'en débattre, de proposer des méthodes de résolution ou encore de soumettre à la classe des problèmes créés par les élèves eux-mêmes. Ces temps collectifs permettent également de contribuer à développer une meilleure expression orale des élèves. Néanmoins, lors des séances de résolution de problèmes, la priorité doit être donnée aux temps pendant lesquels les élèves résolvent effectivement eux-mêmes des problèmes.

La recherche de solutions de problèmes peut être menée à plusieurs, en invitant les élèves à collaborer, par binôme ou par groupes de trois ou quatre élèves. Il est néanmoins nécessaire d'accorder d'abord aux élèves un temps de travail individuel en amont de la mise au travail par groupe, afin de leur permettre de s'approprier le problème chacun à leur rythme et ainsi faciliter l'engagement de tous les élèves dans la tâche de résolution.

Lors des temps de recherche individuelle ou par groupe, l'enseignant doit veiller à circuler dans les rangs pour consulter les productions de chacun des élèves afin de pouvoir :

- encourager leur mise en recherche ;

- relancer le travail des élèves bloqués, pour des raisons mathématiques ou non, en posant des questions pour les aider à s'approprier l'énoncé, en invitant à faire un dessin ou un schéma, en proposant du matériel ;

- inviter des élèves à utiliser les ressources à leur disposition (cahier de référence ou affichages) ;

- demander à des élèves ne trouvant pas la même chose de comparer leurs résultats et leurs procédures pour se mettre d'accord ;

- accompagner plus longuement des élèves ayant des besoins spécifiques ou des difficultés particulières ;

- etc.

« Modéliser » et « calculer » sont deux compétences fondamentales pour la résolution de problèmes à l'école élémentaire qui doivent guider l'action de l'enseignant pour aider les élèves à surmonter leurs difficultés. En effet, lors de la résolution de problèmes, les principales difficultés rencontrées peuvent relever de :

- difficultés à « modéliser » : l'élève n'arrive pas à faire le lien entre le problème posé et le modèle mathématique dont il relève, il ne comprend pas le sens de l'énoncé ou il ne propose pas de solution ou encore la solution proposée ne s'appuie pas sur les opérations attendues ;

- difficultés à « calculer » : les calculs effectués, mentalement ou en les posant, sont erronés, la ou les erreurs pouvant être dues à une méconnaissance de faits numériques ou à une maîtrise imparfaite des algorithmes de calcul utilisés.

On retrouve ces deux cas dans les exemples ci-dessous :

Les actions de remédiation sont fondamentalement différentes dans les deux cas. Dans le premier cas, un travail important devra être mené pour s'assurer que les élèves concernés comprennent effectivement l'énoncé et soient en mesure de le reformuler. Ils peuvent être invités à effectuer une représentation de la situation ou même à reproduire la situation en utilisant un matériel approprié, comme des images représentant les articles achetés et de la monnaie factice. Dans le second cas, la modélisation est correcte, les élèves concernés peuvent simplement être invités à travailler avec d'autres élèves ayant également modélisé correctement la situation, pour vérifier si leurs résultats sont plausibles, comparer les calculs effectués et échanger afin de se mettre d'accord sur le résultat à trouver.

Lors des temps de recherche individuelle, il est important de veiller à ce qu'une sur-sollicitation de l'enseignant par les élèves ayant le plus d'appétence et de facilités pour les mathématiques ne le conduise pas à répartir ses interventions d'une façon qui ne correspondrait pas aux besoins des élèves.

Lors d'une séance de mathématiques, tous les problèmes traités n'ont pas nécessairement besoin de faire l'objet d'une mise en commun en fin de séance. En effet, si tous les élèves ont réussi à traiter de façon satisfaisante un problème donné, la validation de ces réponses dans les cahiers en circulant dans les rangs doit être suffisante. De même, si seuls un ou deux élèves n'ont pas réussi à traiter un problème donné, une action spécifique auprès de ces élèves peut être plus efficace qu'un échange en classe entière.

Si l'objectif fixé en donnant un problème à résoudre est de faire émerger une procédure de résolution particulière ou une représentation-type et qu'aucun élève ne fait ce qui est attendu, l'enseignant ne doit pas renoncer à ce modèle ou attendre qu'il émerge nécessairement d'un élève de la classe. Il peut le proposer lui-même, par exemple en le présentant comme une méthode utilisée par un élève l'année précédente, en invitant les élèves de la classe à discuter de la justesse et de la pertinence de la résolution proposée.

La présentation à la classe d'une proposition de résolution d'un problème peut se faire de façon très efficace grâce aux outils numériques, en projetant sur écran ou tableau numérique la proposition d'un élève et en invitant celui-ci à expliciter oralement sa solution. Ces outils peuvent aussi permettre de projeter plusieurs solutions pour les comparer et permettre à la classe d'évaluer à la fois la justesse des résolutions et leur efficacité. Si la salle de classe n'est pas équipée de façon idéale, d'autres procédures de mises en commun peuvent être envisagées, comme la vidéo-projection d'une photo de la solution d'un élève ou, à défaut, la copie de tout ou partie de la résolution proposée.

4 - L'évaluation des acquis des élèves

Tout au long de la scolarité, des évaluations régulières doivent permettre de s'assurer de l'acquisition, par tous les élèves, des connaissances et compétences relatives à la résolution de problèmes visées par les séquences qui viennent de s'achever, mais aussi de s'assurer que les compétences et connaissances travaillées lors des périodes et années précédentes sont bien toujours présentes.

Conclusion

La résolution de problèmes, au centre de l'activité mathématique, engage les élèves à chercher, émettre des hypothèses, élaborer des stratégies, confronter des idées pour trouver un résultat. Qu'elle soit proposée individuellement ou collectivement en invitant les élèves à collaborer avec leurs pairs, la tâche de résolution de problèmes permet aux élèves d'accéder au plaisir de faire des mathématiques.